Finding the ball
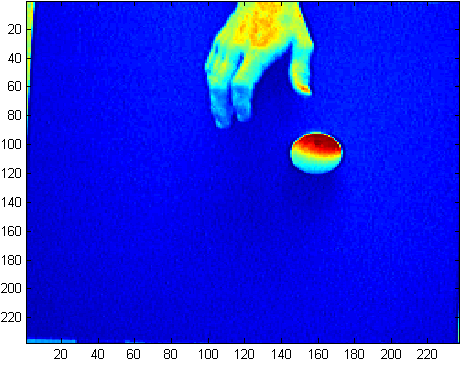
Finding a white ball on a dark surface is child's play. For us.
Computers are a whole ‘nother case. Computers can't see form, they can only see color. While this is helpful in situations such as these (Note: I'm not a big fan of Flash, but this is the first site ever that actually needs Flash and has put it to good use.) most of the time this is a disadvantage. For instance, a white bathroom tile half in bright sunlight, half in shade looks like two totally separate objects to a computer. This can cause serious problems trying to identify a ball, because the computer sees the brightly lit side of the ball as one object, and the dimly lit side and it's shadow as another. So even a white ball on a black background can prove troublesome, as was my case.
In the beginning, on the advice of my professor, Dr. Eric Busvelle, I used a barycenter method, which calculates an image’s “center of gravity” based on weighting of color intensities. This method worked exceedingly well under controlled circumstances, but exactly as I explained above, it ran into show-stopping problems when dealing with varying light conditions. Since the goal of my project was to demonstrate it in various schools and to use it as a lab experiment, this was a major stumbling block.
We tried to solve the problem by having as strong and diffuse a light source as possible, but we always ran into problems. For instance, as the sun advanced across the sky, it shone directly into my lab from 2 to 4PM, making it impossible for the computer to identify the ball. I eventually tried wedging myself into the corner underneath the window sill with a black piece of paper on top shielding the table, but it still wasn't reliable. Worse, all the noise in the signal would make my table shake itself to pieces. Literally.
I even played around with the camera white balance, gain, and aperture time. In the end, it turned out that the best images are taken when the picture is overly dark, with the only identifiable feature the ball.
We still had a speed problem, though. Basically, it boils down to this: classic convolutions are slow. They increase quadratically in processing time with image size. So, taking a 640x480 image and convoluting it with another 640x480 image was incredibly slow. On the order of tens of seconds. We needed our info in under 20ms.
There are four, complementary, solutions to this. First, and most important, to take a smaller picture. With the Matlab algorithm, the best camera resolution that still permits real-time processing is 320x240.
Second, I dramatically reduced the picture that we needed to analyze by cropping the photo down to just the ball. While you might wonder how I can crop the image to the ball's size when I don't even know where the ball is, this was easily enough done by considering that the ball has physical limitations of velocity and that it can't move at light-speed. Thus, my cropped rectangle only has to be the size of the ball + the distance the ball could feasibly move in one step time. Since my step time is 40ms, this distance was on the order of 2cm. So instead of 320x240px, I was only analyzing 70x70px images.
Third, the speed of the convolution is related to not only the image size, but also the image mask that represents the object of interest. So by making the image mask as small as feasibly possible, I decreased the calculation time, too.
Fourth, the Matlab convolution algorithm is very inefficient. Far faster is a FFT convolution, since multiplcation in the frequency domain corresponds to convolution in the time domain. The new algorithm was so much better, I doubled the resolution to 640x480 and still shaved the processing time down to 4ms.
4ms leaves us a very comfortable margin for everything else the computer has to do.