Kinematics

A rolling ball on an inclined plane:
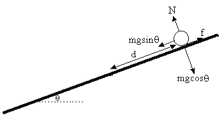
ball on inclined plane
A rolling ball is a classic physics problem, and is quite easy to analyze.

Elementary physics classes teach us that an object sliding down a frictionless inclined plane will accelerate at the rate of:

Pasted Graphic 8

Our problem is a little more complicated, as we can’t measure the acceleration along the inclined plane. Since the camera is mounted perpendicular to the ground, we only know the acceleration in the horizontal directions. We have no direct knowledge of vertical displacement. (In fact, we could calculate this solely from the the image, but we would need very precise information on the perceived size of the ball, data that we simply cannot get with a webcam and plastic lens.)

So what we need is the component of acceleration parallel to the plane's surface. This is easy enough:

Pasted Graphic 7

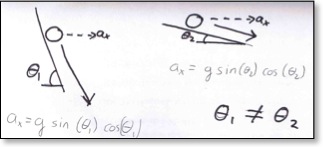
two solutions for rolling ball
NOTE: there are now two solutions for a given observed horizontal acceleration. That is to say, there are two angles the table can be tilted at which will give a same observed acceleration. For example, imagine the plate is perfectly level. The ball will not accelerate horizontally, right? Obviously. Now, imagine that the plate is completely turned on its side, i.e., the ball is falling freely right next to the plate, but the plate is no longer touching the ball. The ball still has no acceleration in the horizontal direction, even though it's accelerating like mad toward the ground.

We solve this ambiguity in a time-honored way: ignoring it. the ambiguity occurs before and after 45deg. As long as we are well away from 45deg, there can be only one solution.

Finally, we need to take into account the fact that the ball is rolling, not sliding. This means that due to rotational inertia the ball won't accelerate, nor decelerate, as quickly as a sliding block on a frictionless surface. The inertial term, however, is quite easy to calculate and add to the equation. Let's call it kt.

Pasted Graphic 6

Where kt=1/(1+2/5) for a sphere of uniform mass distribution.

Of course, we are neglecting friction, but nothing's perfect. In any case, considering the size and material of our pool ball, friction has most likely a pseudo-linear effect on the ball, so all we really need to do is calibrate the ball on a rolling surface and compare it to the expectations.

Which I have done and subsequently included in the kt term. My final kt was about 70% of the theoretic one.

Table kinematics:


Technically, the table has a rotational inertia, too, but this can be neglected as the table is so light in comparison to the servos’ force.
All that's left is to calculate the angle of the table for a given push-rod height.
We start off by analyzing a plane in three dimensions. The equation for a normal vector to a plane going through the origin (0,0,0) can be written as:

Pasted Graphic 5

In order to know the acceleration of the ball, we must calculate THETA, the angle the table makes from the vertical axis.
For this, we'll use classical 3D calculus, done in most sophomore college math classes. We know that:

Pasted Graphic 10

and

Pasted Graphic 11

We want to solving for cos(THETA) and sin(THETA) because the driving equation is:

Pasted Graphic 6

Thus, we have

Pasted Graphic 13

and

Pasted Graphic 12

We chose A=N and B as the unit vector along the z-axis, B= ek. This gives:


Next, we need to break the radial acceleration down into x- and y-acceleration. This is quite easy, and simply requires taking the x component of the acceleration and dotting it with the x-axis, and the y component of the acceleration and dotting it with the y-axis.


Lastly, it might come in handy (and it does later on) to know what z values are required for a given acceleration, instead of knowing what acceleration will result from a given z.
We simply solve the two ax and ay equations for z1 and z2 and then put in z1=u1 and z2=u2. (Since z1 and z2 are the pushrod heights, and the pushrod heights are the controls, we just go ahead and make the substitution) You can do this by hand, but we used maple:


Ball and plate kinematics:


As mentioned in a previous section, a traditional two servo, two-axis table has problems with the “pea and spoon” effect. The three servo system does away with this by always placing the table's axis of rotation underneath the ball.